標準誤差的意義與解釋

中興大學 生物系統工程研究室  陳加忠

此篇文章內容來自Biochemia Medica 2008;18(1):7-13.

一、標準誤差（Standard error）

標準誤差是一個古典的統計量（statistics）。在許多歸納統計中作為輸出結果，但是在敘述統計也有其作用。標準誤差此名詞用以提供一組數據其數值分散的程度。使用標準誤差之基本假設為數據符合中央極限處理。此中央極限處理是所有參數歸納統計技術之假設基礎。在應用時，樣本必須為任意樣本，每個觀察值彼此為獨立。不論其母群的分配是什麼，自此母群取樣的大量任意樣本存在著常態分配。雖然小數目的樣本本身不是常態分配，但是在樣本數目（n）增大時，這些樣本平均值的分配就迅速的趨向常態分配。中央極限定理第二點是n增大之後，樣本平均值的變異就減少。上述之假設十分重要，由這些假設允許研究者藉由抽樣以歸納母群。

由於經費與時間的限制，研究人員無法自有興趣的母群取得許多樣本。因此自樣本得到對處理母群的知識此或然率十分重要。樣本的代表性來自中央極限定理此理論之樣本分佈。標準誤差此統計量可用以估算母群參數所能發現的區間範圍，也可用以代表以樣本統計量代表母群的精確程度。標準誤差愈小，樣本統計量愈接近母群的參數。一個統計研究的標準誤差即是樣本分配中對此統計量的標準差（standard deviation）。

標準誤差（standard error）與標準差（standard deviation）是否不同？這兩個觀念十分相近，但是有不同的使用目的。標準差是用以量測樣本的變異程度。標準誤差是量測樣本分配的變異程度。標準差是用以量測樣本之分散性質。標準誤差是量測樣本分配之分散性質。標準誤差即是在大量樣本自母群被取樣之後，用以代表樣本平均值分散性。

二、平均值的標準誤差（standard error of the mean）

平均值的標準誤差以SE代表

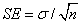
標準誤差（SE）為母群標準差（standard  deviation），除以本數之平方根。因此樣本數目n愈大，標準誤差就愈小。

平均值的標準誤差以σ_M為代表，也可寫成S.E._mean或SEM。

SEM可用以粗略的估算母群平均值的信賴範圍。以SEM乘以1.96，代表母群之樣本其平均值95%之出現範圍。以平均值加或減1.96SEM，即可得到樣本平均值的最大與最小極限範圍。這個上下限數值提供母群平均值可能出現的範圍。在研究中所選擇的信賴水準（通常P<0.05）代表平均值落在此範圍的機率。這種範圍是母群平均值可能出現的信賴區間。為使得信賴區間之計算更為精確，建議使用t分配。

1.96±SEM的另一個用途是決定母群參數是否為0。如果信賴區間的計算值包括零，母群平均值即有可能為或是接近零。

三、估計值之標準誤差（Standard error of the estimte）

估計值的標準誤差（S.E.est）是用以描述回歸分析其預測的變異性。計算公式如下：

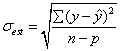
y為樣本量測值，y’為迴歸模式預測值，對樣本而言，

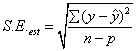
p為模式參數數目

用此σ_est與S.E._est都是用以代表迴歸模式預測的分散程度。S.E._est愈大，代表數據對迴歸線的分散程度愈大。S.E._est愈小，代表數據集中於迴歸線之周圍。

四、其它標準誤差

每一個歸納統計與標準差一定有所關聯。標準差是一個重要的統計量，提供了有關統計分析是否準確的資訊。標準差愈大，統計量的信賴區間也就愈大。信賴區間可廣大至涵蓋所有的量測範圍。當然太大的信賴區間對於母群參數的位置無法提供任何資訊。

統計量的標準誤差與所研究之水準相關，統計量或許不顯著。但是如果樣本數目極大，例如大於1000，自樣本量測結果經計算後可能為顯著。例如樣本數目大於1500，相關數目只有0.01，也有可能顯著。但是如此小的相關（0.01）在臨床醫學或科學研究是無意義。因此相關分析中另一個統計量為有效大小（effect sizes），此數值相當小，但是檢定結果為顯著時，標準偏差即成為一個有效的工具用以決定這種顯著性是來自良好的預測，還是只是樣本數目的影響。

使用標準偏差計算統計量的信賴區間即可協助研究人員進行判斷。例如統計檢定結果為顯著，但是信賴區間涵蓋50%以上的數據範圍，研究者即可判斷此顯著性是沒有意義。因為母群參數的範圍如此廣大，得到之數據對母群沒有任何意義。

統計量如果涉及2個或2個以上的變數（例如迴歸分析、t檢定等），有其他統計量用以協助統計檢定。有用的統計量稱為有效大小（effect size）。例如一個迴歸分析，其樣本大小為1500，顯著性為0.001，其P值為有顯著性。但此種迴歸分析的預測能力是否良好？以有效大小此統計量可以回答此問題。迴歸分析之有效大小統計量稱為Pearson Product Moment Correlation Coefficient,通常稱為Pearson r相關係數，如果r值小於0.3，統計檢定為顯著，但是對實際結果無意義。R = 0.3，代表變數（dependent Variables）對獨立變數（independent variables）之解釋只有9%，9%又稱為決定係數（coefficient of determination, R²），

使用R²之價值在於同時使用Pearson r統計量與估計標準差（standard error of the estimate）。研究人員可以此計算預測的信賴區間，對所有參數相關分析統計與標準誤差都可使用。對於非參數相關分析，計算信賴區間也都可以提供一個粗略的估計以協助研究者進行判斷。這些統計量在一些統計軟體如SAS, STATA或SPSS不一定自動產生，但是可以藉由另一個指令加以運算。

五、結論

標準與標準偏差相近，都是用以量測分散程度之統計量。標準差提供樣本之分散程度；標準偏差則提供樣本分配分散程度之資訊，用以評估母群。以樣本估計值以代表母群估計值時，標準偏差可以用以量測此樣本代表性的準確與精確。如果有效大小此統計量無法獲得，使用標準偏差計算信賴區間則十分重要。標準偏差不只是用以量測評估樣本統計量的分散性與準確性，更是用以評估由此樣本推估母群的可靠性。善用有效大小此統計量，並結合P值與樣本數目，對研究人員幫助極大。研究者藉此可瞭解自任意取樣之樣本，其統計量之可靠性與準確性。