|
Statistical tests, P values, confidence intervals, and power: a guide to
misinterpretations
Sander Greenland, Stephen J. Senn, Kenneth J. Rothman, John B. Carlin,
Charles Poole, Steven N. Goodman, Douglas G. Altman
Eur J Epidemiol (2016) 31:337 – 350
摘要
數十年來，對統計檢定、信賴區間和統計檢定力的誤解和濫用一直受到譴責，但仍然猖獗。一個關鍵問題是，對這些概念沒有簡單、直觀、正確和萬無一失的解釋。相反地，正確使用和解釋這些統計量數據需要注意細節，這似乎會消耗工作科學家的耐心。這種高度認知需求導致了流行簡易定義和解釋，這些定義和解釋完全是錯誤的，有時是災難性的。然而這些誤解在大部分科學文獻中占主導地位。由於這個問題，我們提供了定義和對基本統計量的討論。這些基本統計比通常找到的傳統介紹性概論中，更普遍和更具批判性。我們的目標是為這些對於統計理論和技術知識有限，但希望避免誤解的教師、研究人員和統計使用者提供資源。
我們強調，研究者以他們數據產生P值，用以判結果。對於未說明的分析協議，也可能得到小的P值。即使聲明的檢定假設是正確的，也可能這個假設是不正確的而導致大
P 值。然後，我們提供了對P值、區間和檢定力的25種誤解的解釋性列表。我們總結了改進統計解釋和報告的指南。
介紹
數十年來，對統計檢定的誤解和濫用一直受到譴責，但仍然如此猖獗，以至於一些科學期刊不鼓勵使用“統計顯著性”。不被動根據P值將結果分類為“顯著”或不“顯著”。有一份期刊現在禁止所有統計檢定和數學上相關的程序，例如信賴區間。關於此類禁令的特點導致了大量討論和辯論。
儘管有這樣的禁令，我們預計有爭議的統計方法將在未來很多年還是伴隨我們。因此，我們認為有必要改善基礎教學以及對這些方法的一般理解。為此，我們嘗試以比傳統方式更普遍和批判的方式，解釋顯著性檢定、信賴區間和統計檢定力的含義，然後根據我們的解釋，回顧評論的誤解。
我們還討論一些更微妙的，但仍然普遍存在的問題，解釋為什麼考察和綜合所有的科學結果問題，是如此重要。比起只是涉及個人的發現。我們進一步解釋了為什麼統計檢定，永遠不應該用來作為構成對關聯或影響的推斷或決策的唯一因子。許多原因包括，在大多數科學環境中，將結果任意分類為“顯著”和“不顯著”。對於數據的有效解釋是不必要的，而且往往會破壞數據的有效解釋。與任何其他分類相比，對樣本大小的估計，圍繞我們估計值的不確定性，對於科學推理和合理判斷而言都重要得多。
可以在許多關於統計方法及其解釋的文章、章節和書籍中找到對一般問題的更詳細討論。此篇討論著重共同的關鍵問題：應無假設檢定與統計顯著性。特異性IC問題在長度覆蓋在這些來源，並在任何同行評議的文章。
入門:統計模型、假設和檢定
每種統計推斷方法都取決於複雜假設網路，以關於如何收集和分析數據，以及如何選擇分析結果進行展示。所有假設呈現在支持該方法的統計模型中。該模型是數據可變性的數學表示，因此理想情況下將準確捕獲到此類可變性的所有來源。
然而，由於這種統計模型通常包含不切實際或不合理的假設，因此出現了許多問題。為此甚至包括“非參數”方法，依賴於的假設任意採樣或隨機化。這些假設在數學上寫起來往往看似簡單，但在作業中很難滿足和驗證，因為它們可能取決於成功完成一長串動作，例如識別、聯繫、獲得同意、獲得合作，並追蹤受試者，以及遵守所有位置、masking和數據分析的研究方案。
定義模型的範圍也存在一個嚴重的問題，因為它不僅應該包括觀察到的數據，而且還應該允許關於可能已經觀察到的假設對立數據。“可能已經觀察到的數據此參考框架通常是不清楚的，例如，是否已經量測了多個結果指標或多個預測因素，並且在收集數據之後，就圍繞分析，並且選擇做出了許多決定。
統計模型通常以高度壓縮和抽象的形式呈現，這加劇了瞭解和評估基本假設的難度。因此，許多假設都沒有引起注意，並且經常不被統計數據的使用者所識別。儘管如此，所有的統計方法和解釋都以模型假設為前提，換言之，在該假設模型提供了一種有效的假設，我們期望數據的變異與此假設，忠實地反映情況環境的環繞與發生的現象。
在大多數的統計檢定應用中，一個假設模型是一種假設，有特定效應具有特定大小，並且已針對統計分析進行了定位。為了簡單起見，使用這個詞“效應”。如果因果相關對大多數的調查。這種有針對性的假設，被稱為研究假設或檢定假設，使用的統計方法對其進行評估，稱為統計假設檢定。大多數情況下，目標效應量是一個“虛無”值，代表零效應（例如，研究治療的平均結果沒有影響），在這種情況下，檢定假設被稱為虛無假設。儘管如此，也可以檢定其他效應大小。還可以檢定效應是否落在特定範圍內。例如可能會檢定效應不大於特定量的假設，在這種情況下，假設被稱為是單層的或分開(diriding)的假設。
許多統計教學和作法已經形成了一種強烈而且不健康的觀點。即研究的主要目的應該是檢定虛無假設。事實上，大多數對統計檢定的描述只關注檢定虛無假設，整個主題被稱為“虛無假設顯著性檢定” （NHST）。這種對虛無假設的唯一關注導致了對檢定的誤解。添加到這種誤解是，許多教科書作者（包括RA
Fisher）中使用“虛無假設”來指示代表任何檢定假設，儘管這種用法是在與其他作者不同也與普通英語定義的“虛無不同”，因為這是“顯著性”和“置信度”的統計用法。”
不確定性、概率和統計顯著性
統計分析的一個更精細的目標是提供關於效應大小的確定性或不確定性的評估。很自然的用假設的“概率”來表達這種確定性。然而，在傳統的統計方法中，“概率”不是指假設，而是在假定統計模型下數據模式的假設次數的數量。這些方法因此稱為次數論方法，它們預測的假設次數稱為“次數概率”。”
儘管接受了大量相反的訓練，但許多受過統計教育的科學家將這些次數概率誤解為假設概率。更令人困惑的是，統計學家的保留術語“參數值的近似值”，是指給定參數值的觀察數據其概率，它不是指給予此參數定值的概率。
這些問題最為猖獗是在被稱為
P值的假設頻率，也稱為檢定假設“觀察到的顯著性水準。”上世紀以來，基於這一概念的統計“顯著性檢定”一直是統計分析的核心部分。該重點是傳統定義中P值和統計顯著性，一直應用在虛無假設。所有其他假設是用於計算p值，而被稱為是正確的方法。確認其它假設往往是有問題的，而且也是毫無根據的，我們採取對p值更普遍的看法，作為統計結論兼容。以對於觀測數據預測或期望比對。其前提是整個統計模型（用於計算
P 值的所有假設）都是正確的。
具體而言，數據與模型預測之間的距離是使用檢定統計量（例如t
統計量或卡方統計量）來衡量的。如果每個模型假設與包括檢定假設都是正確，則P值是檢定統計量與其觀察值至少一樣大的概率。
這個定義顯示了，傳統統計所失去的一個關鍵點的定義。在邏輯方面，P值是用以檢定所有的關於假設生成的數據（全模式），而目標不僅僅是只檢定虛無假設。此外這些假設所包括的內容遠遠超過傳統上作為建模或概率假設呈現的內容。這些包括關於分析進行的假設，例如中間分析結果，不是用於確定哪些分析將呈現。
確實如果每個假設都正確P
值越小，數據就越不尋常。但是非常小的 P
值，並不能告訴我們哪個假設是不正確的。例如P值可能非常小，是因為目標假設為假。但是它可能相反非常小，因為違反了研究協議，或者因為它的樣本極小而被選擇用於演示。較大的P值僅是表示數據在模型下沒有異常，但並不代表著模型，或目標假設其任何方面是正確的。它可能很大，因為違反了研究協議，或者因為它被選擇用於展示的樣本數目極大。
P
值的一般定義，可能有助於人們理解為什麼統計檢定告訴我們的，比許多人認為的要少得多。P
值不但不能告訴我們，要檢定的假設是否正確。與該假設具體相關的任何內容，並沒有說明。除非我們可以完全確信，在此研究中用於其計算的所有其他假設都是正確的。然而這是太多研究所缺乏的保證。
儘管如此，P
值可以被視為量測數據與用於計算它的整個模型之間，一個兼容性的連續度量值，範圍從 0(
表示完全不兼容)到 1(
表示完美兼容)。從這個意義上說，可以被視為衡量模型對數據的擬合。然而P值過於頻繁，被降解成為一個二分法，對其中結果宣布為“統計學顯著”。如果P落在或低於臨界值（通常為0.05），並宣布“不顯著”。術語“顯著性水準”和“阿爾法水準” ( )經常用於代表臨界值。而，術語“顯著性水準”會導致將臨界值與
P 值本身混淆。
它們的區別是深遠的。臨界值應該在預先確定，因此是研究設計的一部分。量測數據是保持不變。相對之下，P
值是從數據中計算出的一個數字，因此是一個分析結果，在計算之前是未知的。
從檢定轉為估計
我們可以改變檢定假設，同時保持其他假設不變，以查看 P值在檢定假設競爭之間有何不同。通常，這些檢定假設對目標效應有不同的大小。例如我們可以檢定假設，兩個處理之間所述平均差值是零（虛無假設），或者是20或-10或感興趣的任何數字。
如果檢定中使用的所有其他假設（統計模型l）都是正確的，則此檢定產生
P = 1 的效應，是與數據最兼容的數值。此事對實際觀察到的情況預測，並且提供了在這些假設下對效應的點估計。檢定產生
P > 0.05的效應量，通常會定義一個大小範圍（例如從 11.0 到
19. 5），這將被認為與比範圍外的尺寸數據更兼容（在觀察值更接近預測模型的意義上）。如果統計模型是正確的。該範圍對應於1
- 0.05 = 0.95 或 95 %
信賴區間，並提供了一種總結多種效應的假設檢定結果的便捷方法。信賴區間是區間估計的示例。
Neyman建議以這種方式構建信賴區間，因為它們具有以下特性：如果在有效應用程序中計算95%
的信賴區間。平均而言，其中 95%將包括或覆蓋真實效應大小。因此此指定的信賴水準稱為覆蓋概率。隨著Neyman強調這個覆蓋概率是長序列的屬性，是從有效的模型計算得到。而不是任何只是一個信賴區間。
許多期刊現在需要信賴區間，但大多數教科書和研究僅討論無效假設的P值。這種獨特的重點放在虛無假設不僅誤解檢定，也不了解試驗檢定。也掩蓋了P和信賴區間之間的密切關係值，以及也掩蓋共同的弱點。
P值，信賴區間和檢定力計算沒有告訴我們是什麼？
許多扭曲，源於對
P 值及其相關性（例如信賴區間）的基本誤解。因此，根據我們參考文獻列表中的文章，我們回顧了普遍存在的
P 值誤解，以此作為朝著有依據的解釋和陳述一種方式。我們採用Goodman的格式提供了一份誤解列表，可用於批判性地評估，已有的研究報告和評論所提供的結論。粗體文字的每一個陳述重大統計失真。我們添加強調“不是”強調這些陳述不僅是錯誤的，而且“對於實際目的還不夠真實。”
對單一P值的常見誤解
1 .
P值是檢定假設為真的概率；例如，如果對虛無假設的檢定給出
P = 0.01，則虛無假設只有 1% 為真。相反如果它給出P
= 0.40，則虛無假設有 40% 的概率為真。
不是！P
值假設檢定假設為真？它不是假設概率，可能與檢定假設的任何合理概率相差甚遠。P
值僅表示數據符合測試假設條件及符合測試中使用的所有其他假設（基礎統計模型）預測的模式的程度。因此，P =
0.01 可能表示數據與統計模型（包括檢定假設）預測的不接近程度。而 P = 0.40表示數據更接近模型預測，允許機會變化.
2.虛無假設的P
值是僅是偶然產生觀察到的關聯性的概率。例如，如果虛無假設的 P 值為0.08，則單獨產生關聯性的概率為
8% 。
不是！這是第一個謬誤的常見變體，它同樣是錯誤的。述說單獨的機會產生觀察到的關聯，在邏輯上等同於斷言這些用於計算
P 值的每個假設都是正確的，包括虛無假設。因此要聲稱虛無P
值是單獨產生觀察到的關聯的概率是完全倒退的。
P
值是假設機會單獨運行而計算的概率。通過思考 P
值（從一組假設，例如統計模型推導出的概率）如何可能指代這些假設的概率。可以理解常見反向解釋的荒謬性。
注意：人們經常看到從這個描述中去掉了“單獨” ，變成虛無假設的
P 值是產生觀察到的關聯的概率的機會，因此該陳述更加模棱兩可，但也同樣是錯誤的。
3.一個顯著檢定結果（P > 0.05），代表該試驗假設是錯誤的或應該被拒絕。
不是！一個小P值只是簡單地標記該數據為不尋常的，而且前提就是如果所有的假設（包括測試假定）都是正確的。它可能很小，因為存在一個較大的隨機誤差或是因為他違反了測試假設以外的某些假設（例如p沒有選擇被進行展示，因為它低於
0.05）。P < 0.05 僅代表著與假設預測的差異（例如，n
個處理組之間沒有差異）。只代表造成差異機會例如違反測試假設或錯誤的假設。
4.一種不顯著的檢定結果（P>
0.05），代表其測試假設為真或應該被接受。
不是！如果用於計算P
值的所有假設（包括檢定假設）都是正確的，則較大的 P 值僅表明數據並非異常。
在許多其他假設下，同樣的數據也不會不尋常。此外即使檢定假設是錯誤的，P
值也可能很大，因為它被大的隨機誤差或其他一些錯誤的假設。P > 0.05
僅代表著與假設預測的差異（例如，處理組之間沒有差異）將與觀察到的差異一樣大或大於超過 5%
的機率，如果只是造成差異機會。
5.
大
P 值是支持檢定假設的證據。
不是！事實上，任何的P值小於1代表著測試假設不是最兼容數據，因為任何其他假說較大的P值甚至會更兼容這些數據。一個P值不能說是有利於檢定假設，除非與那些具有較小
P 值的假設有關。此外較大的 P
值通常僅表明數據無法區分許多相互競爭的假設。這些通過檢查信賴區間的範圍可以立即看到。例如，許多作者會將虛無假設檢定中計算得到的P
= 0.70誤解為沒有效果的證據，而實際上它表明，即使虛無假設與用於計算P
的假設下的數據其兼容值，並不是與數據最相符的假設。最相符合將屬於P = 1的假設。但是即使
P = 1，也會有許多其他假設與數據高度一致。不能從一個推導出的P值無論多麼大，因此定義歸納結論的“無關聯”
6.
虛無假設P
值大於0.05代表觀察沒有效果，或者顯示或證明沒有效果。
不是！觀察P > 0.05為無效假設僅表示該虛無是在眾多假設中有P > 0.05。因此，除非點估計值（觀察到的相關性）完全等於虛無值，這是一個自P > 0.05一項研究發現“無關聯”或“沒有證據的”效果的錯誤歸納。如果虛無P
值小於 1 ，則數據中必須存在某種關聯。因此研究人員並且必須查看點估計值，以確定與假設模型下的數據最兼容的效應量。
7.
統計顯著性。表明已檢測到具有科學或實質性重要的關係。
不是！尤其是當研究規模很大時，非常小的效應或很小的違反假設可能會導致對虛無假設的統計顯著性檢定。同樣，如果用於計算數據的所有假設（包括虛無假設）都是正確的，那麼小的虛無P值只是將數據標記為異常；但數據異常的方式可能沒有臨床意義。在給定模型的情況下，必須查看信賴區間以確定哪些科學或其他實質性（例如臨床）重要性的影響大小與數據相對兼容性。
8.
缺乏統計顯著性表明效應量很小。
不是！尤其是當研究數量較小時，即使是較大的效應也可能“淹沒在噪音中” ，從而無法通過統計檢定檢測顯示具有統計顯著性。一個大的虛無P值只是標誌數據不是不存在，而前提是所有的假設（包括測試的假設）是正確的。但同樣的數據任何其他模型和假設下也不會出現異常。同樣，必須查看信賴區間以確定它是否包括重要的效應大小。
9. P
值是我們的數據在檢定假設為真時出現的概率。例如，P = 0.05代表著在測試假設下觀察到的關聯只會發生5%
。
不是！P
值不僅指我們觀察到的，還比我們觀察到的更極端的觀察（其中“極限”代表以特定方式量測）。再次，P值是指在全部用於假設計算數據的次數是正確的。除了檢定假設之外，這些假設還包括抽樣隨機性、處理分配、損失和遺失，以及基於
P 值的大小或結果的其他方面未選擇用於呈現的假設.
10.
如果您因為
P < 0.05而拒絕檢定假設，那麼您出錯的機率（您的“重要發現”是假陽性的機率）為
5%。
不是！要了解為什麼這種描述是錯誤的，假設檢定實際上是正確的。因此如果你拒絕它，你錯誤有機會是100％，不是
5％。5 %
僅指當測試假設和用於測試的所有其他假設都為真時，多次在不同研究中使用測試時，您拒絕它並因此出錯的次數。它不是指您單次使用測試的，它可能已被假設違反以及被隨機錯誤所拋棄。這是誤解
#1 的另一個版本。
11.
P = 0.05
和
P < 0.05 表示同一件事。
不是！這就好比說報告的身高=
2米，與報告的身高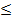 是相同的事情：
“身高 =2m”包括幾個人，這些人將被視為高個子。而“身高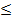= 2m”將包括大部分人，包括小孩子。類似地，P
= 0.05 將被視為統計顯著性方面的臨界結果，而 P < 0.05
此模糊邊界結果以及與模型非常不兼容的結果（例如P = 0.0001）。因此其含義模糊，沒有好的目的。
12.
P值的正確報告為不等式（例如，當
P = 0.015時報告為“ P < 0.02 ”或當
P = 0.06 或 P = 0.70 時報告“ P
> 0.05 ” ）。
不是！這是不好的做法，因為它使讀者難以或不可能準確解釋統計結果。只有當
P 值非常小（例如低於 0.001）時，不等式才變得合理。當用於計算
P值的假設確定性沒有足夠的知識時，非常小的 P
值之間幾乎沒有實際差異。並且大多數計算P 值的方法，在某個點以下在數值上並不準確。
13.
統計顯著性是所研究現象的一種屬性，因此統計檢定可檢測顯著性。
不是！當研究人員聲明他們已經沒有發現具有統計顯著影響的“證據”，就會加劇這種誤解。被測試的效果不是存在，就是不存在。“統計顯著性”是對P
值的二分描述（它低於所選的臨界值），因此是此研究統計檢定結果的一個屬性。它不是研究的效果或人群的屬性。
14.
應始終使用兩尾
P 值。
不是！兩尾P
值目的在檢定目標效應度量值等於特定值（例如，零值）且既不高於也不低於該值的假設。然而，當科學或實際興趣的檢定假設是單尾假設時，單尾的P
值是合適的。例如考慮新藥在延長生存時間方面是否至少與標準藥一樣好，這一實際問題就適合使用單尾P值。
這個問題是單方面的，所以檢定這個假設需要使用單尾
P 值。儘管如此，因為雙邊 P
值是通常的默認值。所以重要的是，要注意何時以及為什麼要使用單尾 P 值。
還有其他對
P 值的解釋的爭議，因為是否是絕對的宣稱“不！”取決於一個人的統計哲學和所涉及術語的確切含義。如果人們希望避免此類爭議，則有爭議的主張值得認識。
例如，有人認為
P 值高估了反對檢定假設的證據，這是基於直接將P 值與特定數量（概似比和Bayes因子）進行比較。這些數據在Bayes分析中作為證據度量值有著核心作用。儘管如此，許多其他統計人員不接受這些數量為黃金標準。而是指出，P值繼總關鍵證據，來衡量根據統計決定錯誤率測試。（即使他們還是遠遠不夠，可以使這些決定）。因此從這個次數論者的角度來看，P
值並沒有誇大證據，甚至可以被視為衡量證據的一個方面其中 1 – P用以衡量與用於計算
P 值的模型相反。
P值比較和預測的常見誤解
統計檢定對科學文獻造成的一些最嚴重的扭曲，涉及不同研究或研究亞組的錯誤比較和綜合結果。其中最糟糕的是：
15.
當在不同的研究中檢定相同的假設，並且沒有或是只有少數檢定具有統計顯著性（所有 P > 0.05）時，所有證據支持該假設。
不是！這種信念經常被用來聲稱當文獻支持無效果時。而研究者在反對對一方。它反映研究者的趨勢“高估大部分的檢定力研究” 。在實際上，每一項研究都有可能無法達到統計學意義，但在統計上顯示出顯著，而且與有說服力的證據相關聯等。例如，如果有5個研究，每個研究P
= 0.10，那麼在 0.05 水準上沒有一個是顯著的。但是，當這些P值是使用組合Fisher公式，整體的P值將在0.0 1。有很多實際的例子，有說服力的證據。一些重要的影響研究甚至沒有研究報告顯示“顯著統計”協會。因此，個別研究缺乏統計顯著性，不應被視為暗示全部支持沒有效果。
16.
當在兩個不同的母群中檢定相同的假設，並得到的 P 值在0.05
的兩邊時，此結果是相互矛盾的。
不是！統計檢定對研究人群之間的許多差異很敏感，這些差異與他們的結果是否一致無關，例如每個比較組的群大小。作為一個結果，兩項研究可以提供非常不同p值。而是假設測試。例如，假設我們有兩個隨機試驗
A和 B 的治療。試驗A與處理組織平均差異值標準誤差為2。而試驗
B與處理組平均差異的標準誤差為1 .如果兩個試驗都觀察到與處理組之間的差異恰好為
3，則通常的正常測試將在A 中產生 P
= 0.13，而在 B 中產生P =
0.003。儘管它們的 P 值存在差異，但對以A與B的影響應該有
P = 1，反映了觀察到的研究平均差異的完美一致性。結果之間的差異必須通過直接評估，例如通過估計和測試這些差異以產生比較結果的信賴區間和
P 值（通常稱為異質性、相互作用或修改的分析）。
17.
當在兩個不同的母群中檢定相同的假設，並獲得相同的 P 值時，結果是一致的。
不是！同樣，測試對母群之間的許多差異很敏感，這些差異與他們的結果是否一致性無關。兩個不同的研究來測試相同的假設甚至可能表現出相同的
P 值，但也表現出明顯不同的觀察關聯。例如，假設隨機試驗A平均差為3.00與標準差為1.0，而B觀察得到12.00的平均差異，而標準誤差4.00。那麼標準的正常測試將在兩者中產生
P = 0.003；然而，對跨研究效應無差異假設的檢定得出 P = 0.03。這樣反映了平均差異之間的巨大差異
(12.00 - 3.00 = 9.00) 。
18.
如果觀察到較小的
P 值。則下一項研究很有可能在相同的假設產生至少同樣小的 P 值。
不是！即使在兩個研究都是獨立的且包括檢定假設在內的所有假設，在兩個研究中都是正確的理想條件下，這也是錯誤的。在這種情況下，如果觀察到
P = 0.03，則新研究顯示 P < 0. 03的可能性僅為
3 %。因此，新研究將P 值顯示為較小或更小的機會，正是觀察到的P
值。另一方面，如果小 P
值的出現僅僅是因為真實效果完全等於其觀察到的估計值，則相同設計的重複實驗將有50%
的機會反而具有更大的 P 值。一般而言，新P
值的大小，將對研究大小以及新研究中違反檢定假設或其他假設的程度極為敏感。特別的是，P可能是非常小或非常大，依賴於研究的違反假設或大或小。
最後，雖然我們希望顯然這樣做是錯誤的，但有時會看到虛無假設與另一個對立假設相比，使用雙邊 P
值作為原值和單邊 P值作為對立。 這種比較是偏向於虛無的，所述兩個雙面測試將錯誤地僅一半拒絕比較經常將虛無作為單尾測試。
信賴區間的常見誤解
大多數上述錯誤解釋都轉化為對信賴區間的類似錯誤解釋。對於例如，另一個 P的解釋力> 0.05的是，它是指在測試假設僅具有是的5％的機率為假。這在一個方面信賴區間成為常見的謬誤：
19.
研究提供的特定
95%信賴區間代表有 95% 的機會包含真實效應量。
不是！報告的信賴區間是兩個數字之間的範圍。觀察到的區間（例如，0.72 – 2.88）包含如果真實效應在區間內，真實效應的次數是
100%，或者否則0%；95 %
僅指出如果用於計算區間的所有假設都是正確的，那麼從非常多的研究中計算出的95%信賴區間包含真實大小的次數。可以計算出一個區間，該區間可以解釋為包含真值的概率為
95% 。儘管如此，此類計算不僅需要用於計算信賴區間的假設，還需要對模型中效應大小的進一步假設。這些進一步的假設總結在所謂的先驗分佈中，結果區間通常稱為Bayesian後驗或可信區間，與信賴區間區分。 對稱地，對於小
P 值誤解為反駁測試假設可以轉化。
20.
超出95%
信賴區間的效應大小，已被數據駁斥或排除。
不是！如同P值，則信賴區間計算從許多假設，違反其中的假設可能導致結果。因此，需要將數據與假設以及任意95%
標準相結合，才能聲明區間外的效應大小，在某種程度上與觀察結果不相容。即便如此，宣稱效應量已被駁斥或排除，這樣極端的判斷將需要更強大的條件。與P值相同，信賴區間可以是極具誤導性。
21.
如果兩個信賴區間重疊，則兩個估計或研究之間的差異不顯著。
不是！來自兩個亞組或研究的
95% 信賴區間可能基本重疊，但它們之間的差異檢定仍可能產生 P < 0.05。
例如，假設來自具有已知變異量的正常母群的平均值的兩個95%
信賴區間為(1.04, 4.96) 和(4.16,
19.84)這些區間重疊，但是對跨研究影響沒有差異的假設檢定，得出P = 0.03。如同P值，兩母群之間的差異性比較，需要統計直接測試和估計各組的差異。使用相同的假設計算信賴區間，如果兩個95％信賴區間未能重疊，我們將發現差異P < 0.05。 如果其中一個95%區包括來自另一組或研究的點估計，我們將發現差異
P < 0.05。最後，與 P 值一樣，信賴區間的複製屬性通常會被誤解。
22.
觀察到的
95 % 信賴區間。預測未來研究中 95% 的估計值將落在觀察區間內。
不是！這種說法在幾個方面是錯誤的。最重要的是，在該模型下，95%
是其他未觀察到的區間包含真實效應的次數，而不是所呈現的區間包含未來估計值的次數。事實上，即使在理想條件下，未來估計落入當前區間的可能性通常也遠低於95%。例如，如果相同數量的兩個獨立研究提供具有相同標準誤差的無偏常態點估計，則第一個研究的
95 % 信賴區間包含來自第二個研究的點估計的可能性為 83 % （即是兩個估計值之間的差異值小於
1.96 標準誤差的機率）。同樣，觀察到的間隔包含或不包含真實效果。95 %
僅指如果用於計算區間的所有假設都是正確的，那麼從非常多的研究中計算出的95%信賴區間包含真實效應的次數。
23.
如果一個
95% 信賴區間包括虛無值而另一個排除該值，則排除虛無值的區間是更精確的區間。
不是！當模型是正確，統計的精確性估計是通過信賴區間直接量測寬度（所量測的相應的標度）。這不是包含或排除虛無值或任何其他值的問題。考慮平均值差異的兩個95%
信賴區間，一個的侷限值為 5 和 40，另一個的侷限值為
-5 和 10。第一個區間不包括零值0，但寬度為
30 個單位。所述第二類包括虛無值，但是是一半寬，因此更加精確。
除了上述誤解之外，95%
的信賴區間迫使讀者採用 0.05 級的臨界值，將所有效應大小與
P 0.05混為一談，這樣就如同將P
值呈現為二分法一樣糟糕。儘管如此，許多作者同意信賴區間優於檢定和 P
值，因為它們允許人們將注意力從虛無假設轉移到與數據兼容的所有效應量範圍。許多作者推薦的這種轉變和增長發表於期刊的數量。另一種方法引起注意非虛無假設是呈現它們的
P 值。例如，人們可以為那些被認為是科學上合理的虛無值對立方案的效應量提供或要求P
值。
與
P 值一樣，需要進一步謹慎以避免將信賴區間誤解為在沒有保證的情況下提供明確的答案。假設點估計是正確的效應，將具有最大的
P 值（在大多數情況下P = 1 ），並且信賴區間內的假設將比區間外的假設具有更高的
P 值。那P值將變化很大。然而，假設在間隔內，如以及假設將間隔外面。此外即使其中一個假設在區間內，而另一個假設在區間外，兩個假設也可能具有幾乎相等的
P 值。因此如果我們使用 P
值來衡量假設與數據的兼容性，並希望將假設與該度量進行比較，我們需要直接檢查它們的 P
值，而不是簡單地詢問假設是在區間內還是區間外。當被檢查的假設之一是虛無假設時，這種需求尤其迫切。
對檢定力的常見誤解
一個試驗的檢定力，是檢測正確的替代假設，而此試驗將拒絕虛無假設之預設可能性。例如P不會超過預先指定的臨界值，例如
0.05的概率。（如果替代假設為正確，未能拒絕檢定假設的相應預研究概率為1檢定力，也稱為II
型或 beta 錯誤率）。與 P
值和信賴區間一樣，此概率是在同一研究設計的重複性上定義的，次數概率也是如此。合理的對立假設的一個來源，是用於計算研究提案中的檢定力的效果大小。因此檢定力的呈現並不排除需要提供區間估計和對立方案的直接測試。
由於這些原因，許多作者譴責使用檢定力來解釋估計值和統計檢定，認為（與信賴區間相反）它分散了對假設的直接比較的注意力，並引入了新的誤解，例如：
24.
如果您接受虛無假設，因為原P
值超過 0.0 5 並且您的檢定檢定力為90
%，那麼您出錯的機率（您的發現為偽陰性的機率）為 10 %。
不是！如果虛無假設為假並且您接受它，那麼您出錯的機率是 100%，而不是
10%。相反，如果虛無假設為真並且您接受它，那麼您出錯的機率為 0 %。10％只是指出在多次試驗中，出錯的機率。而前提是所有使用的其他假設進行測試是正確的研究。它不是指您對測試的單次使用或在任何對立效應量下的錯誤率，而不是用於計算檢定力的效應量。
通過給出一個假設的檢定力或
P 值和另一個假設的檢定力來比較兩個假設的結果可能特別具有誤導性。例如，通過查看P
 0.05的檢定力是否小於
1 - 0.05 = 0.95 來測試虛無值（按照常規做法）會使比較偏向於零值。因為它導致錯誤拒絕的概率較低的虛無假設
(0.05)，而不是在對立方案正確時錯誤地接受虛無假設。因此，關於相對支持或證據的聲明，需要基於對兩個假設的支持或證據的直接和可比較的量測，否則會出現如下錯誤：
25.
如果虛無P
值超過 0.05 並且該測試的檢定力為
90% 在對立方案中，此結果支持虛無假設勝過對立假設。
不是！這種說法對許多人來說似乎很直觀，但反例很容易構建，其中虛無P 值在
0.05 和 0.10 之間。但也有對立假設，其自身的
P 值超過 0.10 ，其檢定力為
0.90。
儘管它在解釋當前數據方面存在缺陷，但它對於設計研究和理解為什麼即使在理想條件下“統計顯著性”的複製也經常失敗是有用的。當使用
0. 05 顯著性水準時，研究通常被設計或聲稱具有 80%
的效力，以對抗關鍵對立方案，儘管在執行中由於諸如低受試者招募等意外問題通常具有較小的檢定力。因此，如果備選方案是正確的，並且兩項研究的實際檢定力為80%，那麼兩項研究都顯示P 0.05
的機會最多僅為
0.80 (0.80) = 64%。此外一項研究顯示 P 0.05
而其他研究沒有（因此會被誤解為顯示相互矛盾的結果）的可能性是 2(0.80)0.20 = 32 %
或大約 3分之1
的可能性。類似的計算考慮到典型的問題表明，人們可以預見到“複製的危機” ，甚至如果沒有出版文獻或報告偏見，只是因為目前的設計和檢定對單個研究結果是二元輸出：“顯著” / “不顯著”或“拒絕” / “接受” 。
統計模型不是只有一個帶有希臘字母的方程式。
現在將轉向直接討論一個最近受到更多關注，但在統計教學和演示中仍然被廣泛忽視，或過於狹隘解釋的問題：用於獲得結果的統計模型是正確的。很多時候，完整的統計模型被視為一個簡單的迴歸或結構方程，其中影響的參數表示由希臘字母表示。“模型 檢查”然後被僅限於檢定配適性或檢定模型的附加項。然而，這些配適檢定本身做出了進一步的假設，這些假設應該被視為完整模型的一部分。例如，所有常見的檢定和信賴區間都取決於對觀察或處理的隨機選擇，以及在控制共變數水準內的隨機丟失或遺失。這些假設已經通過敏感性和偏差分析逐漸受到審查，但這些方法與基本統計特徵相去甚遠。
大多數研究人員。其分析本身並沒有朝著引導發現不顯著或顯著（分析偏差），並且他們將分析結果的效果沒有基於他們發現的不顯著或顯著（報告偏倚和發表偏倚）。即使是統計顯著性、P值和信賴區間的有其理想意義，研究者選擇性的報告也會導致錯誤。由於研究者決定是否報告和編輯決定是否刊載，往往取決於P是否值高於或低於0.05，選擇性報告在科學期刊已成為一個主要問題。
雖然這個選擇問題也受到敏感性分析的影響，但在報告和發表存在此偏倚。通常假設這些偏倚偏向具有顯著性結果。通常是這種情況是研究人員選擇在
P < 0.05時要展示的結果。這種假設當然是正確的，然而這種做法往往會誇大關聯。對於贊成報告要有P < 0.05此偏差的不是證據或支持的常識。例如，人們可能期望在那些與接受虛無假設有關的資助的出版物中選擇P > 0.05。而這種做法往往會低估關聯。數據調查，一些實證研究發現較小的估計和“ 不顯著 ”在這樣期刊往往顯示高於其他的研究期刊。
解決這些問題需要更多的政治意願和努力，而不是解決統計的誤解。例如強制註冊試驗，以及來公布開放所有已完成研究的數據和分析代碼（如AllTrials倡議，http://www.
alltrials.net/ ）。同時，建議讀者在解釋報告提供的統計數據和結論時，考慮研究報告產生和出現的整個期刊背景。
結論
在意識到統計檢定通常被誤解後，人們可能想知道這些檢定是否對科學有什麼幫助。它們最初的目的是將隨機變異性解釋為錯誤的來源，從而提醒人們不要將觀察到的數據關聯過度解釋為真實的影響，或者作為反對虛無假設的更有力的證據。但不久之後，這種用法就被顛倒過來，對於虛無假設提供錯誤支持以“未能達到”的統計顯著性的形式表示。
毫不懷疑，現代統計檢定的創始人會被他們發明的常見處理方法嚇壞。在他們第一篇論文，描述他們的二進制統計檢定方法，Neyman和Pearson寫道，“懷疑是否明知 P值為確實0.03或0.06，而不是0.05。將在事實上，不斷修改我們判斷和檢定本身沒有給出最終裁決，但是可作為工具，幫助使用它們的人形成他的最終決定。
Peason後來補充說：“毫無疑問，我們可以更恰當地說，他的最終或臨時決定。”Fisher進一步說，“沒有一個科學工作者年復一年，有一個固定的顯著性水準。而在這個水準上，在任何情況下，都會拒絕假設。他寧願根據他的證據和他的想法，對每個特定的案例進行思考。”然而，對檢定的錯誤和儀式性使用繼續蔓延，包括認為"
P是高於還是低於 0.05"是一個發現的普遍仲裁者。因此到1965年，Hill嘆道：“無論
P 的值如何，我們常常削弱我們解釋數據和做出合理決定的能力。而且我們常常從‘無顯著差異’推斷‘無差異’。作為回應，有人爭辯說，這一些誤解在已被充分理解的系統上進行嚴格控制的實驗中是無害的。在這些實驗中，檢定假設可能得到既定理論（例如孟德爾遺傳學）的特殊支持，並且其中的所有其他假設（例如作為隨機分配）通過仔細的設計和執行研究而被保持。但長期以來，人們一直斷言，在更不可控和不定形的研究環境（如社會科學、健康和醫學領域）中進行統計檢定的危害遠遠超過其好處，導致呼籲在研究報告中禁止此類檢定，一個期刊禁止再次使用
P 值以及信賴區間。
然而，由於統計檢定的根深蒂固，以及缺乏普遍接受的對立方法。有許多嘗試通過將
P 值從顯著性檢定中的使用中分離出來來挽救 P 值。如前所述，有一種方法是將
P值作為兼容性的連續度量。
儘管這種方法有其自身的局限性（如第 1、2、5、9、15、1、8、19點所述），但它避免將P
值與任意臨界值（如 0.05）進行比較（如第3、4、
6 – 8、10 – 13、15、16、21
和 23 – 25）。另一種方法是教導和使用
P 值與假設概率的正確關係。在常用的統計模型，單尾P值可以提供有關效應的方向假設更低的概率界限。無論如何，這樣的重新解釋，能否可以最終取代良好的效應共同誤解還有待觀察。
將重點從假設檢定轉向估計，已被推廣為一種簡單且相對安全的作業改進方法。期刊編輯對它們的需求從而導致越來越多地使用信賴區間。儘管如此，這種轉變已經引起了對信賴區間的誤解，例如上面的19 - 23 。其他方法將虛無值檢定與涉及虛無假設和對立假設的進一步計算相結合。然而，這種計算可能會帶來與上述檢定利類似的進一步誤解，以及更大的複雜性。
同時，為了盡量減少當前做法的危害，我們可以為統計數據的用戶和讀者提供一些指導方針，並再次強調我們的誤解列表中的一些關鍵警告：
(a)對統計檢定的正確和仔細解釋需要檢查效應估計值和信賴區間的大小，以及精確的
P值（不僅僅是P值是否高於或低於
0.05 或其他臨界值）。
(b)認真解讀所有要求嚴格審查的用於統計分析的假設和公約。不只是一般的統計假設。包括如何選擇表示的結果隱藏的假設。
(c)統計上不顯著的結果而聲稱其支持檢定假設是完全錯誤的。因為相同的結果也可能更符合對立假設。即使這些對立假設的檢定力很高。
(d)區間隔估計用以協助評估數據是否能夠判別不同處理間關於有效大小或是數據能夠以其他假設更好的解釋時，此統計結果是否被誤解。然而警告說，信賴區間通常只是這些任務的第一步。為了根據數據和統計模型比較假設，可能需要計算每個假設的
P值（或相對近似性）。我們進一步警告說，信賴區間僅是用來提供數據留下的不確定性或模糊性的最佳度量情況，因為它們依賴於不確定的統計模型。
(e)多項研究的正確統計評估需要匯總(Pooled)分析或巨量(meta)分析，以正確處理研究偏差。然而即使這樣做了，所有早先的注意事項仍然適用。此外，任何統計程序的結果，只是在檢查全部證據時，必須評估的許多考慮因素之一。在特定的意義上，統計顯著既不是必要性的決定，也並無足夠用以決定一組數據的科學或實際的顯著性。這一觀點得到了美國最高法院的一致肯定（Matrixx Initiati ves,
Inc., et al. v. Siracusano et al. No. 09 – 1156. Argued January 10,
2011, Decided 2011, March 22 ）。也可以在我們之前引用的Neyman和
Pearson 的意見中可以看到。
(f)任何關於假設的概率、可能性、確定性或類似性質的意見都不能只有從統計方法中得出。在特定的，顯著性檢定和信賴區間，本身不提供邏輯堅實的基礎，以歸納一種效應，而關於存在或不存在，與確定性或給定可能性。每當人們看到一個結論是對假設的概率、可能性或確定性的陳述時，就應該牢記這一點。必須使用超出分析數據和傳統統計模型（僅給出數據概率）中包含的假設的資訊，來得出這樣的結論。這些資訊應該明確承認和描述數據提供的結論。
Bayesian統計提供的方法，企圖納入所需的直接資訊進入統計模型。然而，它們還沒有如同達到P值和信賴區間的普及。部分原因是哲學上的反對，部分原因是沒有為它們的使用建立共同的約定。
(g)所有統計方法無論是次數論還是Bayesian，或用於檢定或估計，或用於推理或決策，都對於導致所呈現結果的事件序列做出廣泛假設。不僅在數據生成中，而且在在分析選擇。因此，允許批判性的評價，研究報告（包括巨量分析）應詳細說明事件導致完整序列統計表現，包括研究對象動機，其研究設計，原來的分析計劃，該使用和排除受試者和數據，並對於進行的研究徹底描述所有的進行。
最後，我們注意到沒有任何統計方法可以避免誤解和誤用，但謹慎的統計用戶將避免使用特別容易被嚴重濫用的方法。在這方面，我們同行挑出的p值，特別是對統計作業作為降解成“顯著”和“不顯著，進行討論。 |
