|
European Science
Editing, November 2013; 39(4) 92-94,
Author: Farrokh
Habibzadeh
介紹
在過去的幾十年中,統計方法迅速發展,並在研究論文的數據分析中發揮了重要作用。因此,當前大多數期刊都要求作者在該方法章節單獨詳細描述用於分析其數據的統計方法。這是對論文有幫助的,因為可用以檢查文章中提出的結果發現其內部有效性。在這篇評論中,基於20多年的編輯和審稿經驗,此文章將描述在投稿給生物醫學期刊的稿件中,遇到的最常見錯誤。在著名和小型醫學期刊的投稿稿件中或多或少發現這些相似錯誤。這些許多錯誤也可以在已發表的文章中找到。這意味著即使有些編輯者也沒有意識到這些錯誤要點。
數據分佈
投稿的許多稿件涉及對連續變量的分析,例如年齡,血液pH值和血清膽固醇水平。常見錯誤之一是對所有此類變量進行相同處理。許多作者將它們以平均值和標準差(SD)表示,並通過參數檢驗(例如Student's
t檢驗)進行比較。但是,分析這些數據的最基本步驟之一就是確定這些變量是否呈常態分佈1。應該將常態分佈變量表示為平均值和SD;非常態分佈變量應表示為中位數和四分位數範圍(IQR)-第25和第75個百分位數之間的距離2。參數檢驗(例如,學生t檢驗和單因子變方分析[ANOVA])應為用於常態分佈變量的分析,因為分佈的常態性是這些檢驗所做出的基本假設之一,違反常態分佈將導致錯誤的結果3。不具有常態分佈的變量應與非參數進行比較測試,例如Mann-Whitney
U檢驗和Kruskal-Wallis。但是我們應該如何測試變量是否具有正態分佈?
單樣本Kolmogorov-Smirnov檢驗是可以使用的最受歡迎的(非參數)統計檢驗之一。
但是,作為有用的經驗法則(無需訪問原始數據,這對於審閱者和編輯者非常有用),如果SD超過平均值的一半,則變量的分佈不太可能是常態分配。
SD與SEM
投稿稿件(甚至在已發表的文章中)的另一個常見錯誤是使用平均值標準誤差(SEM)而不是SD標準差來表示數據分散。SEM總是小於SD。因為它是SD除以樣本大小的平方根。一些作者不恰當地使用SEM而不是SD,來顯示他們的需求分散程度較低。
SEM實際上是平均值分佈的SD,因此它是用以量測平均值的精確度。
假設您測量了225名健康男性的空腹血糖,發現平均血糖水準為90
mg / dL,SD為15
mg / dL。假設變量具有常態分佈,因此,預計將近95%的研究樣本(214
= 0.95×225人)的血糖在60(90
– 2×15)mg
/ dL和120(90
+ 2×15)mg
/ dL之間。因為根據常態分佈的特徵,即在常態分佈中,有95%的數據在平均值±2×SD之內。假設樣本代表母體。然後我們可以指出,研究人群中95%的人的血糖水準在60到120
mg / dL之間。那當然有幫助。但是假設我們的研究人員研究了900人而不是225人,得出的平均值(90
mg / dL)和SD(15
mg / dL)都是相同。會有什麼改變?我們的陳述將與以前完全相同。同樣,根據獲得的結果,我們可以指出,研究人群中95%的人的血糖濃度在60到120
mg / dL之間。正如您大多數人的直覺所知,唯一的區別是:當您量測900人時,結果比量測225人時所獲得的結果更為精確。
假設我們嘗試對225人進行100次研究。也就是說要對225人進行100次採樣,以測量他們的血糖。
然後我們將有100個均值(和100個SD)。
當然,這100個平均值將不會完全相等,而是圍繞一個數字(平均值的平均值)分佈。該“平均值”是與真實總體平均值最接近的可能值。
要檢查這100個平均值在其“平均值”附近的分散水準,我們可以計算其SD。
可以證明SEM是對該SD的很好估計1,3。幸運的是,對於此SD的推導,我們不需要運行100次實驗,我們可以簡單地從一個實驗中得出的SD進行計算(
15 mg / dL)。
如前所述,參加225人的研究的SEM是:
SEM=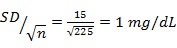
對於參加900人的研究,SEM是:
SEM=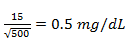
無論變量在樣本中的分佈如何,平均值的分佈通常都是常態的。因此,考慮到常態分佈的特徵,平均值的所有可能值的95%,都在平均值的近2倍SEM之內。
換句話說,此間隔是平均值的95%信賴區間(95%CI)。
這意味著在我們的例子,對於225名參與者的研究(概率為95%),總體的實際平均值將在98(100
– 2×1)mg
/ dL和102(100
+ 2×1)mg/dL之間。
900名參與者的平均95%CI為99至101
mg / dL。現在很明顯,對於900名參與者(2
= 101–99 mg / dL),平均值的95%CI是225名參與者(4
= 102–98 mg / dL)平均值的一半。與參加225人的研究相比,參加900人的研究的精確度更高。它只是表明要使精確度提高一倍,我們應該將樣本大小增加四倍(22)(900
= 4×225)。
SEM實際上不是衡量研究變量離散程度的方法。它是一種指示平均值精確度的數值。在科學寫作中,當我們要提出數據分散性的度量時,應該使用SD,而要提出測量平均值的精確度時,我們應該提供SEM。標準誤差並不是針對平均值,我們也可以針對其他統計數據(例如,優勢比(OR),相對風險和百分比(例如,患病率和發生率))進行計算。這就是為什麼通常將這些統計信息與95%CI一起報告的原因2。不要忘記95%CI與標準誤差密切相關,並且可以簡單地從另一個中計算得出。但是我們通常報告95%CI,而不是標準誤差。但是,標準誤差可以用作圖形中的誤差線,以表示量測的準確性。
報告統計數據不恰當的準確性
我們報告統計數據的精確度應取決於我們的測量精度。例如,在一項針對成年人的研究中,我們通常以年為單位記錄年齡,因為通常更精確地測量年齡對臨床研究沒有影響。但是在同一項研究中,由於血液pH值的微小變化與嚴重的臨床結果有相關,因此我們可以用小數點後兩位甚至三位數字來量測血液pH值。但是無論原始數據的測量精確度如何,統計軟體通常都以預定的精確度來計算結果,例如小數點後三位。因此除非修正此預測值,否則軟體會報導上述變量的平均值,即年齡和血液pH值至小數點後三位。在投稿的稿件中,閱讀“患者的平均年齡為37.351歲”這樣的陳述很少見。報告年齡的單位為一年的千分之一(將近9個小時)時,這代表著我們向參與研究者詢問了他們的出生時間。但是,我們通常只詢問他們的出生年份。上述平均值可能應報告為“
37”或“
37.4”年,而不用再精確。對於表示平均值和標準差的數字位數尚無共識。雖然可以從數學上顯示出平均值和標準差應以原始數據量測中所使用的準確度報告。但一些權威學者認為應以多一位數字報告它們4,5。
百分比也類似。
“在35名參與者中,有12名(34.29%)發燒”,這種發燒患病率應寫為“
34%”。因為當增加或減少35名參與者中的一名參與者時,該百分比幾乎改變了3%。報導中出現0.29
%為不合理。因此根據經驗,當參與者總數(分母)等於或小於100時(或者,當百分比值超過參與者數目時,我們不應報告任何小數點後的數字。當參與者人數等於或小於20時,最好不要完全報告百分比,因為這可能會產生誤導5。此外,最好報導百分比的95%CI,尤其是如果主要結果。因此以上陳述應該表示為:“在35名參與者中,有12名(34%;
95%CI:18–51%)發燒。”從另一個角度來看,當考慮95%CI的寬度時,以較高的精度報告患病率看起來是不合理的。
報導p值
在某些稿件中,作者報告的p值為p
<0.05,p>
0.05或p
= NS。許多權威人士認為,最好報告p值的確切值,例如p
= 0.023,p
= 0.647。以前,從統計表中內差以計算p值,因此很難確定其確切值。但是,目前統計軟體程序會報告p的確定值。有時當p值非常小(例如0.00001)時,該軟體僅在小數點後三位報告該數值,因此該軟體將其顯示為“
0.000”。因此作者錯誤地將其報告為p
= 0.000或更差的值p
<0.000。
p值是一個概率,因此可以從最小的零到最大的1
變化。如果P值為1或0,則事件肯定是會發生或不會發生。但是,在實驗研究中,我們永遠無法確定是0或1。因此,實際上我們面對的p值大於。(不等於0)且小於(不等於1)。因此,如果軟件體的p值為0.000,則正確表示應為p
<0.001。由於p值是概率,因此它永遠不能為負。因此p永遠不能表示為<0.000。報告p值時,小數點後的報告不必多於三位數。一些期刊可能會要求您也報告所使用的統計檢驗數值,例如Pearson
χ2= 1.796,df
= 3;
p =
0.62。
95%信賴區間與p值
有時,稿件同時呈現p值和95%CI作為統計數據。例如我們可能會看到諸如“吸煙顯著(p
= 0.04)與更高的肺癌發生率(OR
= 2.6; 95%,CI:1.3–5.2)相關聯”的陳述。當母群中確實沒有這種差異(I型錯誤)時,p值只能表示偶然觀察到有差異性的可能性。它沒有提供有關變化量的任何信息,即所謂的效果大小。另一方面,95%CI不僅告訴我們效應的大小,而且還告訴我們差異是否具有統計學意義(例如,對於OR,如果95%CI不包含1,則差異顯著)。對於上面的示例,OR的95%CI(1.3-5.2)表示,以95%的概率,該風險不小於非吸煙者的1.3倍且不大於5.2倍,因此由效應大小當中,由於95%的CI不包含1,因此表明吸煙對肺癌的發生率有重大影響。因此沒有必要同時提及p值和95%CI。有後者就足夠了,該聲明可以寫成“吸煙與肺癌發生率更高相關(OR
= 2.6;
95%CI:1.3-5.2)。”
有時候情況更糟;
p值與95%CI相矛盾。
語句“(OR
= 3.1; 95%CI:0.97–9.91,p
<0.05)”具有內部不一致。儘管p顯著,但OR的95%CI包含1,這是不可能的。
其他不可能的語句是“(OR
= 4.3; 95%CI:1.12–16.51;
p = 0.06)”,其中p值不重要,但95%CI不包含1。這些錯誤在表中更常見於投稿(和出版)的稿件。
使用p值和95%CI的總體趨勢,只是使用後者。
最小樣本量的計算
在許多試驗報告中,都說明了研究的人數,但沒有提供計算最小樣本量的必要信息。例如,在患病率研究中,作者通常在計算患病率時沒有提供預期的疾病發生頻率和可以接受的誤差。或在臨床試驗中,作者通常無法提供對他們重要的(具有臨床重要性的)最小變化,效應量和變量的預期SD。這樣就不可能計算出最小樣本量。
這些問題通常是由於未能足夠詳細地描述研究假設因而引起的。例如,在許多投稿的稿件中,可能會讀到“我們的假設是,在減輕腰痛方面,藥物X比藥物Y更好。更好的假設是“與藥物Y相比,藥物X可將機械性下背痛的女性的疼痛評分降低至少20%(根據視覺模擬量表進行衡量)”,其中研究人群(機械性下腰痛的女性),結果(疼痛評分下降),量測(通過視覺模擬量表)和預期效果大小(20%)都進行了描述。
有時,我們會收到具有描述性的研究,例如有關某個地區瘧疾流行的研究。在此類研究中,由於通常沒有假設,因此不需要統計檢驗。但是,有些作者試圖通過不適當使用統計檢驗和p值來修飾此類稿件。不當使用統計檢驗的另一個例子是,當我們檢查人口的所有成員而不是樣本時。
與不適當的樣本量密切相關的另一個問題是區分“臨床意義”和“統計意義”的問題。有時,我們閱讀的稿件發現統計學上的差異並不具有臨床意義。例如,我們讀到“研究組的平均血清膽固醇水平(189
mg / dL)顯著地(p
= 0.031)比對照組(187
mg / dL)高”。這種差異儘管具有統計學意義,但在臨床上沒有任何意義,並且可能是所研究樣本量超出必須樣本量的結果。因此,在計算最小樣本量時要考慮臨床重要性的差異。招聘超過必要人數的人員可能會導致觀察到差異,儘管差異具有統計學意義,但無臨床意義。除了不道德外,研究參與者小於最小樣本量的可能會導致II型錯誤。
我們之所以可以得出統計上有意義的結果,而總體中不存在實際差異性(I型錯誤)的另一個原因是,在數據分析中進行了多次比較。
例如,如果我們要通過學生的t檢驗比較每兩個組來比較五個組的均值,則需要運行10個測試。
即使五個研究組之間沒有真正的差異,幾乎有40%的概率,我們也會得出具有統計學意義的p值。這個問題可以通過使用適當的測試(例如單向方差分析)來解決,也可以通過為多個比較以校正p的臨界值(例如,使用Bonferroni校正)來解決。
非顯著p值
在投送的稿件中,有時我們會遇到諸如“男性的空腹血糖水平(97.3
mg / dL)高於女性的空腹血糖水平(90.1
mg / dL),但是差異很小(p
= 0.057)”。選擇了臨界值0.05(概率為20的1),以區分“顯著”和“非顯著”差異。實際上,為臨界值選擇“
0.05”是沒有邏輯依據的。但是,當我們選擇0.05的臨界值(這在生物醫學科學中很常見)時,我們就不能再談論“邊緣顯著”,“部分顯著”,或差異是顯著的(p
<0.05)或不顯著。在稿件的討論中,我們有時會遇到類似“……的區別,但是差異在統計學上不顯著(p
= 0.057)”的說法。如果我們招募了更多的人,差異可能會變得很大。我相信這是不可接受的,因為作者大概計算了研究的最小樣本量並招募了必要的參與者。
如果p值不顯著,則可能是由於總體上確實沒有差異,或者該研究未能獲得總體中存在的實際差異(II型錯誤)所致。因此不重要的p值不能用來簡單地解釋為總體中的“無差異”。
相反,作者/審稿人應進行檢定力分析,以確定研究檢定力,並查看研究是否能夠在總體上確實存在差異時檢測出差異3。如果正確確定了最小樣本量,則我們可以
有信心認為研究的檢定力也是正確的。
結論
投稿期刊的稿件,甚至是一些已發表的文章,在數據分析和表示中都存在統計錯誤。
掌握良好的統計知識將有助於編輯,審稿人和作者更好地評估研究。結果這篇評論涉及一些最常見的錯誤。是建議作者應該更詳細地檢查每個錯誤。
參考文獻
References
1. Spatz
C, Johnston
JO.
Basic
Statistics:
Tales
of
Distribution.
4th
ed.California,
Brooks/Cole
Publishing
Co.,
1989.
2.
Bowers
D,
House
A,
Owens
D.
Understanding
Clinical
Papers.
New
York,
John
Wiley
&
Sons,
2002.
3.
Glantz
SA.
Primer
of
Biostatistics.
5th
ed.
New
York,
McGraw-Hill,
2002.
4.
Lang
TA,
Secic M.
How
to
Report
Statistics
in Medicine:
Annotated
Guidelines
for
Authors,
Editors,
and
Reviewers.
2nd
ed.
Philadelphia,American
College
of
Physicians,
2006.
5.
Peat
J,
Elliot
E,
Baur
L,
Keena
V.
Scientific
Writing:
Easy when
you
know
how.
London,
BMJ
Publishing
Group,
2002.
|